Historia del Cálculo

¿Que es el cálculo?

Es la rama de las matemáticas que se ocupa del estudio de los incrementos en las variables, pendientes de curvas, valores máximo y mínimo de funciones y de la determinación de longitudes, áreas y volúmenes. Su uso es muy extenso, sobre todo en ciencias como las económicas y las  ingenierías, siempre que haya cantidades que varíen de forma continua.

Los antiguos pensadores pusieron las bases de las matemáticas y del cálculo que hoy conocemos y todo surge por la necesidad de tener un conteo exacto de las cosas y es por esto que distintos personajes científicos y filósofos aportaron ciertas ideas para que las formulas y procesos matemáticos pudieran existir.

 Entre los principales precursores del cálculo tenemos a los siguientes:

Isaac Newton (04/01/1643-31/03/1727)

En 1664, descubrió los elementos del cálculo diferencial, que llamaba fluxiones. Años más tarde, cuando se publicaron sus hallazgos, hubo cierta duda acerca de si el matemático alemán Leibniz era considerado el creador del cálculo diferencial. Al parecer ambos, independiente y casi simultáneamente, hicieron este notable descubrimiento.  

Generalizó los métodos que se habían utilizado para trazar líneas tangentes a curvas y para calcular el área encerrada bajo una curva, y descubrió que los dos procedimientos eran operaciones inversas. Uniéndolos en lo que él llamó el método de las fluxiones, Newton desarrolló en el otoño de 1666 lo que se conoce hoy como cálculo, un método nuevo y poderoso que situó a las matemáticas modernas por encima del nivel de la geometría griega.

En 1711, publicó diversos libros relacionados al Cálculo como analysi per aequationes numero terminorum infinitas. También, esta relación entre series y cálculo se manifiesta en Methodus fluxionum et serierum infinitorum (escrito en 1671), y publicado en inglés en 1736 y en latín en 1742.

El único libro en que Newton mostró su cálculo y publicó rápidamente fue Philosophiae naturalis principia matemática (1687). 

Newton comparte con Leibniz el crédito por el desarrollo del cálculo integral y diferencial, que utilizó para formular sus leyes de la física. También contribuyó en otras áreas de la matemática, desarrollando el teorema del binomio y las fórmulas de Newton-Cotes.

Desde finales de 1664 trabajó intensamente en diferentes problemas matemáticos. Abordó entonces el teorema del binomio.

Teorema generalizado del binomio (Newton)

 Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita

 Newton había descubierto los principios de su cálculo diferencial e integral hacia 1665-1666 y, durante el decenio siguiente, elaboró al menos tres enfoques diferentes de su nuevo análisis.

Newton y Leibniz protagonizaron una agria polémica sobre la autoría del desarrollo de esta rama de la matemática. Los historiadores de la ciencia consideran que ambos desarrollaron el cálculo independientemente, si bien la notación de Leibniz era mejor y la formulación de Newton se aplicaba mejor a problemas prácticos. La polémica dividió aún más a los matemáticos británicos y continentales, sin embargo esta separación no fue tan profunda como para que Newton y Leibniz dejaran de intercambiar resultados. 

Gottfried Willhem Leibniz (01/07/1646-14/11/1716)

Fue el otro inventor del cálculo. Su descubrimiento fue posterior al de Newton, aunque Leibnitz fue el primero en publicar el invento. En 1673, luego de estudiar los tratados de Pascal, Leibnitz se convence que los problemas inversos de tangentes y los de cuadraturas eran equivalentes.   Alejándose de estos problemas, a partir de sumas y diferencias de sucesiones comienza a desarrollar toda una teoría de sumas y diferencias infinitesimales que acabarían en la gestación de su cálculo

Leibniz fue entonces impresionante, ya que le llevó al descubrimiento del cálculo en 1675 y su elaboración y publicación en dos cortos artículos del Acta Eruditorum después en 1684 y 1686, el primero sobre cálculo diferencial y el segundo sobre cálculo integral., las reglas para la manipulación de los símbolos  "Descripción: y la diferencial. Esto refleja sus ideas filosóficas de buscar un lenguaje simbólico y operacional para representar los conceptos e ideas del pensamiento de tal manera que los razonamientos y argumentos se puedan escribir por símbolos y fórmulas.

En 1684, publica detalles de su Cálculo diferencial en Nova Methodus pro Maximis et Minimis, item que Tangentibus (Nuevos Métodos para Máximos y Mínimos y para las Tangentes). En este artículo aparece la conocida flotación d para las derivadas, las reglas de las derivadas de las potencias, productos y cocientes. Pero no habla demostraciones.
Expuso los principios del calculo infinitesimal; resolviendo el problema de la isócrona & de algunas otras aplicaciones mecánicas; utilizando ecuaciones diferenciales. La mayor aportación de este ilustre personaje fue la aportación del nombre de calculo diferencial e integral; así como la invención de símbolos matematicos para la mejor explicación del cálculo; como el signo = asi como su notación para las derivadas dx/dy & su notación para las integrales. 

En Leibnizl interés no era la aplicación física. De hecho, se podría establecer una correlación entre infinitesimales y "mónadas'', estos últimos entes primarios en la descripción de lo real según la filosofía que aparece en su libro de filosofía (metafísica) Monadología.

El énfasis de Newton era la razón de cambio, mientras que en Leibniz lo era la suma infinita de infinitesimales.

En la historia del cálculo se encuentra la controversia de quién fue el inventor del cálculo, si Newton o Leibniz, algunos le dan la primicia a Newton y otros a Leibniz, pero se generaliza que Newton tuvo primero las ideas y que Leibniz las descubrió igualmente algunos años más tarde. Pero sin duda Leibniz merece igual crédito que Newton, por lo tanto sus aportaciones al cálculo fueron sobresalientes. Leibniz estableció la resolución de los problemas para los máximos y los mínimos, así como de las tangentes, esto dentro del cálculo diferencial; dentro del cálculo integral logró la resolución del problema para hallar la curva cuya subtangente es constante. Expuso los principios del cálculo infinitesimal, resolviendo el problema de la isócrona (ver biografía de Bernoulli) y de algunas otras aplicaciones mecánicas, utilizando ecuaciones diferenciales.

No cabe duda que su mayor aportación fue el nombre de cálculo diferencial e integral, así como la invención de símbolos matemáticos para la mejor explicación del cálculo, como el signo = (igual), así como su notación para las derivadas dx/dy, y su notación para las integrales.

Pierre de Fermat (1601/08/17-1665/01/12)

Las principales aportaciones de Fermat a las matemáticas se produjeron en el campo de la teoría de números. Algunas de ellas son las siguientes: 1. Los números de Fermat: Quizás el gran error del matemático francés. Conjeturó que todos los números de la forma , con natural, eran primos, lo cual resultó ser falso. Fue Euler quien se encargó de refutar esta conjetura descomponiendo así: 2. La factorización de Fermat: Método de factorización ideado por él mismo. 3. El método del descenso infinito: Método de demostración desarrollado por Fermat que seguro le fue muy útil para demostrar muchas de sus proposiciones. Pierre estaba muy orgulloso de él. 4. Estudios sobre números primos, números perfectos y números amigos: Entre ellos posiblemente el más interesante sea el pequeño teorema de Fermat, que después generalizó Euler. También descubrió que los números y eran números amigos. 5. Avances en la ecuación de Pell. 7. Estudios sobre números poligonales: Culminados posiblemente en el siguiente resultado: Todo número puede ser escrito como suma de tres números triangulares, o cuatro cuadrados, o cinco números pentagonales, o seis números hexagonales, y así hasta el infinito. FERMAT Y EL CÁLCULO DE PROBABILIDADES También en este campo influyó el matemático francés. Tanto que se considera a Fermat y Pascal como los precursores del cálculo de probabilidades. El juego que estudiaron en principio era tipo el siguiente: Supongamos que dos amigos, Juan y Antonio, están jugando a un juego y acuerdan que si Juan gana dos partidas gana el juego. Por el contrario Antonio debe ganar tres partidas para vencer. Roberval aseguraba que las probabilidades estaban en proporción 6 contra 4. Fermat y Pascal detectaron el error de Roberval y lo corrigieron. A LAS PUERTAS DEL CÁLCULO DIFERENCIAL Y INTEGRAL Históricamente se considera a Newton y Leibniz como los desarrolladores del cálculo diferencial. Lo que mucha gente no sabe es que puede considerarse a Fermat como el precursor de dicha rama. Fermat estudió la existencia de máximos y mínimos imponiendo que la tangente a la gráfica de la función fuera paralela al eje de abscisas. LA GEOMETRÍA ANALÍTICA También históricamente se considera a Descartes como el desarrollador de la geometría analítica. Pero también en este campo picó Fermat. Introdujo, independientemente de Descartes, las coordenadas para el estudio de problemas geométricos, pudiéndose a partir de entonces utilizar el álgebra para resolverlos. Quizá el mayor acierto de Fermat, y en eso radica su genio, fue entender que cualquier ecuación algebraica con dos variables indeterminadas provoca una única curva geométrica. Con esto probó que la ecuación de una recta que pasa por el origen es de la forma , encontró la ecuación de una circunferencia centrada en el origen, la de una hipérbola referida a sus asíntotas, de una parábola referente al diámetro y la tangente en su extremo y la de la elipse también en un caso concreto.

Leonhard Euler (15/04/1707-18/09/1783)

Leonhard Euler reconocido matemático, filósofo y físico del siglo XVIII que aportó conocimientos fundamentales en el área del cálculo, introduciendo terminología y notación matemática moderna para lograr un mejor análisis matemático.

Aportes

Es importante ver como personajes de siglos anteriores pudieron desarrollar una gran capacidad intelectual para descubrir y/o inventar algunas cosas que serian el principio y el provecho de la sociedad de ahora. Los aportes de Leonhard Euler son utilizados tanto en la matemática pura y en la aplicada, también mencionando que dejo su legado en otras materias como la física y la astronomía. (ver articulo: Jose Saramago)

Algunos filósofos y personalidades importantes del siglo XVIII realizaron el reconocimiento de las obras de Leonhard Euler; además de su capacidad para memorizar gran cantidad de información tras sufrir una terrible enfermedad que le quitó la visión por completo. Entre las aportaciones de Leonhard Euler que deja como legado, se encuentran los siguientes:

Aportaciones al cálculo

Las aportaciones de Euler para el año 1748 fue que realizó una obra de gran importancia ya que escribe uno de sus tres tratados sobre cálculo: Introductio in Analysi Infinitorum en este libro se muestra resultados sobre desarrollos y aportes de los principales conceptos que habían obtenido Leibniz, Bernoulli e Isaac Newtonsus predecesores.

Esta obra de Euler aportes se encuentra escrita en francés, alemán e inglés. De esta manera en este escrito se recoge los siguientes resultados:

Realizó la introducción del concepto de logaritmo, en la que hace una interpretación como un exponente por primera vez.


introduce el numero e en el capítulo VII de la obra.

realiza la prueba de algunas funciones trigonométricas, por ejemplo: sin2 x + cos2 x = y sin(a + b) = sin a cos b + sin b cos a

La ecuación como resultado de un estudio de exponentes imaginarios.

formaliza la definición de función en el capítulo IV de esta obra en la que indica: “Una función de cantidad variable es una expresión analítica formada de cualquier manera por esta cantidad variable y por números o cantidades constantes”. A pesar de no ser utilizado propiamente en la actualidad, para la época fue de gran ayuda para el tratamiento del cálculo infinitesimal independiente de la geometría, como punto central del mejor matemático del siglo XVIII.

Hace el estudio de algunas series, pero se enfoca más en las series de potencias y la relación que tiene con el producto infinito, que se puede ver en los capítulos IV, XIII y XVII del libro.

Johann Bernoulli (27/07/1667-01/01/1748)

La integración fue vista por Johann Bernoulli, simplemente como la operación inversa de diferenciación y, con esta aproximación  el obtuvo muchos éxitos integrando ecuaciones diferenciales.

Sumó series y descubrió teoremas adicionales para funciones trigonométricas e hiperbólicas.

Johann Bernoulli tuvo su mayor forma en vida y fue electo como miembro de las academias de parís, Berlín Londres  Bolonia etc.

 Aplicó a muchos problemas de geometría, ecuaciones diferenciales y mecánica. En 1695, se le designó como profesor de matemáticas y física en Groningen, Holanda y, al morir su hermano Jacques, lo sucedió como profesor en Basilea. De 1691 a 1692 escribió dos pequeños libros de texto sobre el cálculo diferencial e integral, que no fueron publicados; sino hasta mucho tiempo después. El de cálculo diferencial fue impreso hasta 1924 y el de cálculo integral apareció cincuenta años después de que fue escrito, en su Opera omnia de 1742. En 1696, Jean Bernoulli, como desafío para los matemáticos de Europa, propuso el problema de determinar qué curva proporcionaría el tiempo más breve posible de descenso. Esta curva se conoce como braquistócrona (de la palabra griega brachistos, el más corto, y cronos, tiempo). El problema fue resuelto por Newton y Leibniz, así como por los hermanos Jacques y Jean Bernoulli, nietos del refugiado de Amberes. La solución de Jean fue la más elegante; algunos autores se refieren a esa maravillosa solución como una obra de arte, de orden muy elevado, para este difícil problema. Además de su interés, el problema de la braquistócrona tiene gran importancia, ya que fue la fuente histórica del cálculo de variaciones, una rama poderosa del análisis para el estudio del mundo físico. Una exposición de la solución de Jean, para este problema, puede encontrarse en el libro Ecuaciones Diferenciales con aplicaciones y notas históricas de George F. Simmons, en la que se aprecian la interconexión de varios campos y conceptos del conocimiento, como son: Óptica, la Ley de Refracción de Snell, el Principio del Menor Esfuerzo de Fermat, Mecánica, el Principio de Conservación de la Energía y el Cálculo. Estando en París en 1692, instruyó a G. F. A. de L´Hospital (1661-1704) en el cálculo de Leibniz y firmó un pacto bajo el cuál, en reciprocidad por un salario regular, enviaría a L´Hospital sus descubrimientos en matemáticas. El resultado es que una de las principales contribuciones de Bernoulli, de 1694, se conoce desde entonces como regla de L´Hospital sobre formas indeterminadas. Bernoulli encontró que si f(x) y g(x) son funciones diferenciables en x = a tales que f(a) = 0 y g(a) = 0 y.

Esta regla fue incorporada por L´Hospital en el primer libro de texto sobre el cálculo diferencial: Analyse des infiniment petits, publicado por él en París en 1696. Escribió sobre muchos aspectos avanzados de análisis: la isocrona, sólidos de mínima resistencia, la catenaria, la tractriz, trayectorias, curvas cáusticas, problemas isoperimétricos. Contribuyó a la geometría diferencial a través de su trabajo sobre líneas geodésicas en una superficie. Se le atribuye también el cálculo exponencial, porque, además de las curvas exponenciales simples y = a x , estudió exponenciales generales como y = x x . Para el área bajo la curva y = x x , de x = 0 a x = 1, encontró la representación en serie infinita

En 1702, a través de ecuaciones diferenciales, descubrió la relación con lo que apreció relaciones entre funciones trigonométricas inversas y logaritmos imaginarios.

Jakob Bernoulli (27/12/1654-16/08/1705)

Las primeras contribuciones importantes de Jacob Bernoulli fueron unos documentos sobre los paralelismos entre la lógica y el álgebra publicados en 1685, un trabajo sobre probabilidad en 1685 y otro sobre geometría en 1687. Sus resultados en geometría proporcionaron un sistema para dividir cualquier triángulo en cuatro partes iguales con dos líneas perpendiculares. Ya en 1689 había publicado importantes trabajos sobre las series infinitesimales y su ley sobre los grandes números en teoría de probabilidades. En mayo de 1960, publicado en un documento de Acta Eruditorum, demostró que el problema de determinar el isocrono es equivalente a resolver una ecuación diferencial no lineal de primer orden. Tras encontrar la ecuación diferencial, Bernoulli la resolvió mediante lo que hoy llamamos separación de variables. El documento de Bernoulli de 1690 es importante para la historia del cálculo, porque el término integral aparece por primera vez con su significado de integración. En 1696 Bernoulli resolvió la ecuación que hoy llamamos 'Ecuación de Bernoulli' Jacob Bernoulli también descubrió un método general para determinar la evoluta de una curva como envoltorio de sus círculos de curvatura. También examinó las curvas caústicas y en particular estudió estas curvas asociadas a la parábola, la espiral logarítmica y las epicicloides alrededor de 1694. El lemniscato de Bernoulli fue concebido por primera vez por Jacob Bernoulli en 1694. En 1695 investigó el problema del puente colgante que busca el ángulo necesario para que la curvatura del cable mantenga siempre el equilibrio del puente colgante. El trabajo más original de Jacob Bernoulli fue Ars Conjectandi publicado en Basilea en 1713, ocho años antes de su muerte,. El trabajo se hallaba incompleto en el momento de su muerte pero aun así es un documento de la mayor importancia dentro de la teoría de probabilidades. Bernoulli fue uno de los promotores más significativos de los métodos formales del análisis profundo. La astucia y la elegancia se encuentran muy a menudo en su método de presentación y expresión, pero con un máximo de integridad.

Joseph Lagrange

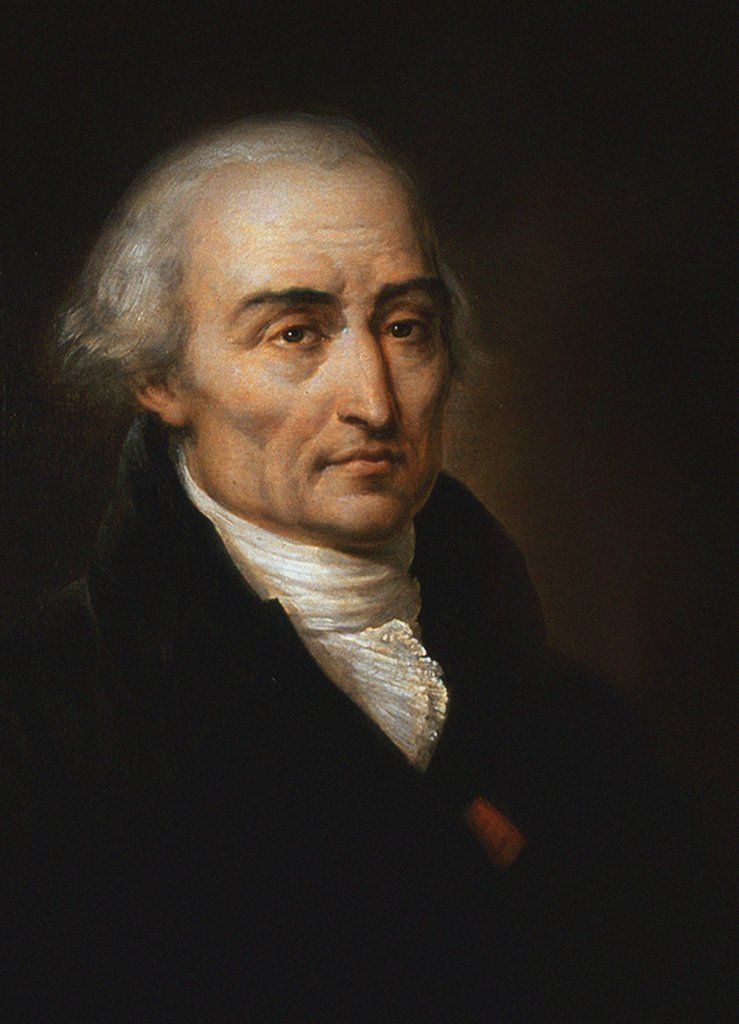
Inventó y maduró el cálculo de variaciones y más tarde lo aplicó a una nueva disciplina la Mecánica Celestial, sobre todo al hallazgo de mejores soluciones al Problema de tres cuerpos. También contribuyó significativamente con la solución numérica y algebraica de ecuaciones y con la teoría numérica. En su clásica Mecanique analytique (mecánicas Analíticas, 1788), transformó la mecánicas en una rama del análisis matemático. Una de las preocupaciones centrales de Lagrange fueron los fundamentos de cálculo.

Obtuvo, entre otros resultados, una ecuación diferencial general del movimiento y su adaptación para el caso particular del movimiento rectilíneo y la solución a muchos problemas de dinámica mediante el cálculo de variantes. Escribió así mismo numerosos artículos sobre cálculo integral y las ecuaciones diferenciales generales del movimiento de tres cuerpos sometidos a fuerzas de atracción mutuas.

Principales aportes a la matemáticas  Teorema del valor medio de Lagrange.

·         Fue el padre y creador del cálculo de variaciones.

·         Multiplicadores de Lagrange.

·         Polinomio de Lagrange.

·         Encontró la solución completa del problema de una cuerda que vibra transversalmente.

·         Creó la idea de ecuaciones generalizadas de movimiento, ecuaciones que demostró formalmente.

·         Descubrió los llamados puntos de Lagrange (astronomía).

·         Teoría del movimiento planetario.

·         Teoría de eliminación de parámetros.

·         Solución completa de una ecuación binomial de cualquier grado.

·         Contribuyó al cálculo de diferencias finitas con la fórmula de interpolación de Lagrange.

 Aportes a la Teoría de Números y la resolución de ecuaciones algebraicas, que sentaron las bases para la teoría de grupos.

Jean Le Rond D´Alembert (16/11/1717-29/10/1783)

Fue uno de los primeros en comprender la importancia de las funciones y en este artículo definió la derivada de una función como el límite de los cuocientes de los incrementos.

D’Alembert fue el que más se acercó a una definición precisa de límite y de derivada. Más en realidad toda duda se desvanecía ante el éxito de sus aplicaciones, de manera que el cálculo infinitesimal, más que una rama de la matemática, se convertía en una especie de doncella de la ciencia natural, en un auxiliar muy valioso, pero auxiliar al fin de las varias ramas de la física.

Su obra maestra fue el tratado de dinámica, donde enunció el teorema que lleva su nombre (principio de d'Alembert). El Teorem Fundamental del Álgebra recibe en algunos países de Europa el nombre de teorema de d'Alembert - Gauss dado que d'Alembert fue el primero en dar una prueba casi completa sobre dicho teorema

Augustin Cauchy (21/08/1789-23/05/1857)

Cauchy resolvió el problema de Poinsot, generalización del teorema de Euler sobre los poliedros. Un año más tarde, publicaría una memoria sobre el cálculo de las funciones simétricas y el número de valores que una función puede adquirir cuando se permutan de todas las maneras posibles las cantidades que encierra. En 1814, apareció su memoria fundamental sobre las integrales definidas y luego abordando el teorema de Fermat sobre los números poligonales, llegó a demostrarlo, cosa que no pudieron Euler, Legendre, Lagrange, ni Gauss. Uno de los mayores triunfos lo obtuvo dando vigor a las demostraciones de Lagrange, ateniéndose al cálculo de ceros e infinitos y fijando las convergencias de las series del análisis.

Algunas de sus obras relacionadas con el cálculo son el Traité de calcul diferentiel et integral (Tratado del cálculo diferencial e integral), Leçons sur la aplication du calcul infinitesimal á la géometrie (Lecciones sobre la aplicación del cálculo infinitesimal a la geometría), Sur les integrales definies prises entre des limites imaginaires (Sobre las integrales definidas tomadas entre límites imaginarios), Sur la aplication du calcul des residus á la solution des problèmes des Physique matématique (Sobre la aplicación del cálculo a la resolución de problemas físico-matemáticos), y Sur un nouveau calcul des limites (Sobre un nuevo cálculo de límites)

Karl Weierstrass (31/10/1815-19/02/1897)

Weierstrass estaba interesado en la solidez de cálculo. En ese momento, no había definiciones un tanto ambiguas respecto a las bases de cálculo, teoremas y por lo tanto, importantes no pudieron ser probados con suficiente rigor. Mientras Bolzano había elaborado una definición razonablemente riguroso de un límite ya en 1817 su obra permaneció desconocida para la mayor parte de la comunidad matemática hasta años más tarde, y muchos tenían sólo definiciones vagas de límites y continuidad de funciones. Cauchy dio una forma de la definición de límite, en el contexto de la definición formal del derivado, en la década de 1820, pero no distingue correctamente entre la continuidad en un punto frente a la continuidad uniforme sobre un intervalo, debido a la insuficiente rigor. Cabe destacar que en el 1821 Cours d'analyse, Cauchy dio una prueba famosa incorrecta de que el límite de funciones continuas es continua en sí. Lo correcto es más bien que el límite uniforme de funciones uniformemente continua es uniformemente continua. Esto requiere que el concepto de convergencia uniforme, que se observó por primera vez por el consejero de Weierstrass, Christoph Gudermann, en un documento de 1838, donde Gudermann señalar el fenómeno, pero no se definen ni desarrolla en él. Weierstrass vio la importancia del concepto, y ambos se formalizaron y se aplica ampliamente a través de las bases de cálculo. La definición formal de continuidad de una función, tal como se formula por Weierstrass, es como sigue: Usando esta definición y el concepto de convergencia uniforme, Weierstrass fue capaz de escribir las pruebas de varios teoremas entonces no probados, como el teorema de valor intermedio, el teorema de Bolzano-Weierstrass, y Heine-Borel teorema. Weierstrass también hizo avances significativos en el campo de la cálculo de variaciones. Utilizando el aparato de análisis que él ayudó a desarrollar, Weierstrass fue capaz de dar una completa reformulación de la teoría que allanó el camino para el estudio moderno del cálculo de variaciones. Entre los varios axiomas importantes, Weierstrass estableció una condición necesaria para la existencia de una fuerte extrema de los problemas variacionales. También ayudó a diseñar la condición de Weierstrass-Erdmann que dan condiciones suficientes para un extremal tener un rincón junto a extrema dado, y le permite a uno encontrar una curva de minimización de una integral dada.

  Vídeo sobre la historia del calculo:

Integrantes:

*Lizette Toledano Apolinar
*Jesús Herrera Bello 
*Erick Guarneros Mendez
*Gildardo Ventura Bello